高校に入ってからも数学が得意な子の特徴は
- 計算スピードが速くて正確
- 理解を伴わせて暗記をしている
- 問題の意味を把握し推論できる
- 言葉・数式を用いて説明できる
この4点が備わっていることだと思います。
理解を伴わせて暗記をする
公立中学で習うレベルの数学であれば、上の4つがすべてができていなくても
なんとなく授業を聞いて問題を解いていれば
つまり普通に勉強をしていれば
フクトで偏差値60前後は取れるようにはなります。
しかし高校になると
公立中学で解いていたものと比較すると式が複雑になるので、計算スピードが遅く正確性が乏しければ、計算問題ですら解けなくなります。
また、覚える公式が多いので、理解を伴わせて覚えていなければすぐに忘れてしまいます。
たとえばa3+b3の因数分解公式は頻繁に使うので(a+b)(a2+ab+b2)を丸暗記しておけば特に問題を解くときに苦労はしないのですが
次のような問題を解くときはどうしますか?
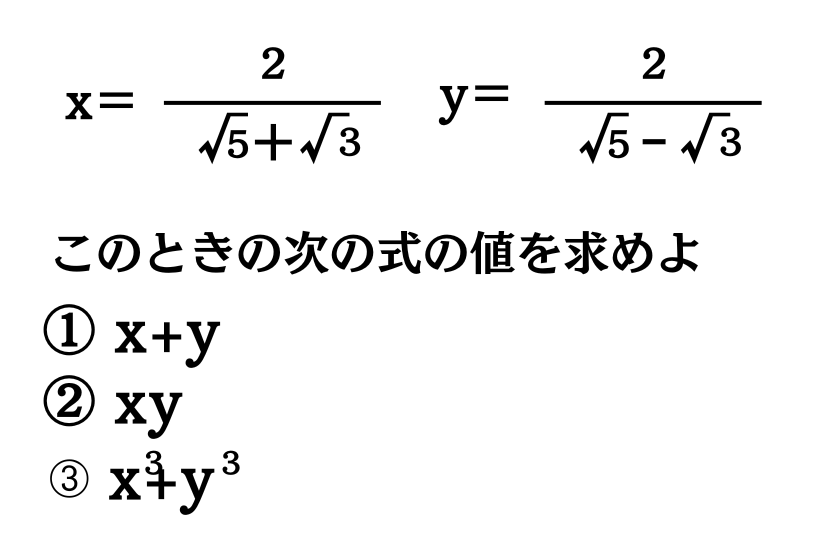
この問題を学校の授業で初めて習うとき
おそらく
「基本対象式(a+b,と ab)で表して計算しましょう」と言われ
①・②を解いた後➂はa3+b3=(a+b)3-3ab(a+b)に変形して解くように教えられているはずです。
中学時代必死に勉強をしているのにフクトの数学で偏差値50くらいしか取れていなかった場合はこの時点でかなり怪しくなるかもしれません。
偏差値60くらいは取れていたのなら公式を丸暗記することで定期テストでは余裕をもって解けると思います。
しかし、フクトで偏差値60を取れていても「数学が得意じゃない」子はかなりいて、そういう子が数か月後に同じような問題を解こうとすると
「う~ん確か因数分解公式じゃないものがあったような???どうだっけ」
と地道に解き始めたりするわけです(それで解ければまだましですが、解けないことの方が多いと思います)。
一方、数学が得意な子(国立大学2次の問題をある程度解けるようになる子)は
「式の中で文字を入れ替えても元の式と同じになる」ものが「対称式」
たとえば「2a+3ab+2b」この式の文字を入れ替えると「2b+3ba+2a」で元の式と同じになるからこれは「対称式」だ。
「対象式は必ず基本対称式で表せる」から『a3+b3』は対象式だから、必ず基本対象式にできる」
「この問題は因数分解公式を使わず対象式の基本公式を利用すればいいはずだから『(a+b)(a2+ab+b2)』ではなく『(a+b)3-3ab(a+b)』この公式だ」
と瞬時にひらめきます。
数学が得意な子が2文字の対称式変形の基本公式「a3+b3=(a+b)3-3ab(a+b)」がパッと出てくるのは「基本対称式、a+bとabで表せる」ということをしっかりと覚えているからだと思います。
この部分を自分の頭に落とし込んで理解することをせず、単に公式の丸暗記をするから「あれ?公式どうだっけ?」となるような、数学を苦手とする子とは異なります。
大学入試は上で示した公式は基本中の基本で、これよりも理解が難しいものが数多くあります。
国立大学を受験する場合は受験期になって焦って「教えてください」「できるようになりたいです」といっても、ほとんどの場合手遅れです。
なぜなら受験科目は数学だけでなく、国語・英語もあるからです。
大学入試は公立高校入試のように半年くらいの努力でどうにかなるのとは次元が異なるので、その点はしっかりと理解しておきましょう。
数学は暗記
具体的にやること
もし、高校でも数学が出来るようになりたいのであれば
理屈で覚えていつでもすぐに思い出せる、つまり、公式を使いこなせるようになることを心掛けてください。
それに加えて「質問内容を理解して回答の流れをイメージする(推論して証明する)」ことが国立大学の入試問題を解くために必要になります。
この部分は個人差が大きいので、
- 特に意識しなくてもできてしまう
- 普段数学に時間をかけているから偏差値60以上はキープできている
- 定期テストは満点近い点数を取れるが実力テストになると偏差値60にすら届かない
- 計算問題以外全く手が付けられない
- 計算問題すらできない
人によって様々な状況が考えられます。
確実に言えるのは
数学が得意だと勘違いし、高校進学後「授業を適当に受け、家でも復習をしない」ようでは進研模試ですら偏差値50を取れなくなるということです。
数学が出来るようになりたいのなら
- 学校の授業をしっかりと聞いて、教科書の例題を確実に解けるようにする
- 網羅系の問題集を解く
- 添削が必要な問題は添削してもらう
高校1・2年次にはこれを徹底してください。
もう少し細かく書くと
- 教科書の例題は学校の授業中に可能な限り理解し、その日のうちに網羅系の参考書で復習をする
- 使う参考書はチャート式の白・黄レベルのもので十分
- 添削が必要な問題は先生にお願いし、解答・解説を読んでも理解ができないものは先生・数学が得意な友達から教えてもらう
- ある程度ペースが出来て時間に余裕が生まれてからは思考力を問う問題や出題分野が明記されていない問題にも挑戦する
こんなところです。
思考力を問う問題や出題分野が明記されていない問題は大学入試の過去問を使うのが一番だと思います(模試だけでは足りないと感じているなら絶対にお勧め)。
過去問を解くためには少なくとも数Ⅱ・Bまでは終わらせておく必要があるので、できれば高校2年の夏休みが終わるころまでに終わらせておきましょう。
私が現役の高校生であれば、数Ⅱ・Bまでを2年の夏休みまでに終わらせ、福大・西南の入試問題を解いて肩慣らしをします。
実際の入試問題に触れることで
- 今の自分が出来ること
- 自分に足りないもの
が見えてくるので、高校3年になるまでにどういう勉強をすればいいかも自ずと見えてくるからです。
これらを実践しても、できるようになる気配を全く感じない(進研模試で偏差値60にも届かない)こともあります。
その場合は数学の配点が少ない国立大学か私立文系大学に進路を決めたほうがいいかもしれません。
数学は個人差が大きく出る科目なので、できない人はできる人の10倍努力してもできるようにはならないからです。

