数学は、論理・抽象概念・空間認知において、個々の理解度や思考力の差が結果に大きく反映されます。
このことから、個人差を考慮した丁寧な指導が重要になる科目といえます。
苦手意識を持っている子は特に塾をうまく活用してください。
目次
授業の進め方
平均前後の子は受け身で勉強していることも多く、丁寧に説明すればするほど集中力が欠け授業を聞けなくなる傾向が見られます。
一方、学年上位の子は「分かり切ったことを解説せずに早く問題を解きたい。そして難しい問題の解説を重視してもらいたい」と感じることが多いです。
こういったことを考慮して、レイズでは要点を絞って簡潔に説明をし、演習中心の授業を行っています。
進め方は以下の通りです。
- 「解説➜類題練習問題」を繰り返し、その日の授業で定着させたい内容を一通り終わらせる
- 「基本問題」を解いて習った内容を解けるか確認
- 「標準問題」を解いて習った内容を解けるだけでなく理解できているかを確認
「基本問題」は「類題練習問題」と同程度のレベルで、授業内容を大まかに理解していれば解答できる問題です。
これらの問題が解けるようになれば、定期テストレベルの問題はほぼ対応できるようになります。
「標準問題」は内容を理解していなければ解けない問題です。
これらの問題が解けるようであれば、福岡県の公立高校入試における同単元の問題も十分に解答できる実力が備わっていると考えて問題ありません。
授業形式
解説と類題練習問題は一斉指導でクラス全員に同じ内容をやってもらいます。
「基本問題」と「標準問題」の演習では、生徒一人ひとりが自分のペースで問題に取り組み、分からない箇所があれば個別にヒントや解説を受けられるようにしています。
このやり方により、自力で問題を解き進められる生徒は、どんどん先に進むことができます。
一方で、じっくりと時間をかけて問題に取り組みたい生徒は、自分のペースで一つずつ理解を深めながら解き進めることができます。
苦手意識を持っている生徒は、通常の授業だけでは克服できないことがあるかもしれません。
その場合は「個別対応」で、それぞれの理解度に合わせて丁寧に指導し「基本問題」までは解けるようにしていきます。
苦手な子は「できていない原因」を把握することが大切
レイズでは、数学が苦手な生徒に対しては、「なぜ問題が解けないのか」の原因の特定から始めています。
数学の得意・不得意は個人差が大きく、原因が単純な「勉強量」とは限りません。
また、「できない」原因は生徒によって大きく異なるため、他の科目のように「これをやれば必ず伸びる」という明確な解決策を示すことが難しいです。
さらに厄介なのは、数学を苦手とする生徒自身が、何が原因で問題が解けないのかを把握できていないことです。
原因を特定できないまま闇雲に勉強しても、的外れなことに時間を費やし、努力しても結果に結びつかず、いつまでも苦手を克服できないままになります。
だから、数学で思うように結果が出せていない生徒が、まず取り組むべきは『できていない原因を把握すること』なんです。
計算問題で間違えが多い原因が「分数の計算ができていない」と分かれば小学生の計算問題
2次関数が解けない原因が「方程式の移項ができていない」と分かれば中学1年の計算問題
図形問題で「公式の暗記ができていない」と分かれば、公式暗記と定着のために問題演習
こういったことは数学が苦手な子が自力でやるのは難しいはずなので、塾をうまく利用してください。
計算ミスの原因
多項式の計算で頻繁に起こるミスの一例

不正解①:分数の前にマイナスの記号があるのに記号を変え忘れて「+3b」にするところを「-3b」にしている
不正解②:通分するときに掛けた数を分子に掛け忘れている
不正解➂:分数の足し算・引き算では分母を消すことができないのに勝手に消している。
1次方程式で頻繁に起こるミスの一例

「記号を変えてそのまま移行」「逆数をかけて移項」このどちらかをはっきりと覚えていないことで引き起こされます。
計算ミスは本当にミスなの?
数学が得意な子と得意でない子に見られる違い
塾生に対して授業でどのようなことを行っているのかを基に数学が得意な子とそうでない子に見られる違いを書いています。
この違いを知ることで、数学に苦手意識を持つ子が問題を解けるようになるために何をすべきかが見えてくるはずです。
ぜひ参考にしてください。
中学2年で中途入塾をしてきた子が「関数が苦手です」といっている場合、「式の計算」「方程式」の計算が定着していないことが原因であることがほとんどなので、塾ではそれらができているかどうかを最初に確認します。
それが原因でない場合、次に考えられる原因は1次関数の基本を押さえているかどうかです。
例えば
- 1次関数の式はy=ax+bで表せる
- aの部分は「変化の割合」or「傾き」という
- bの部分は「切片」という
- 変化の割合はXの増加量分のyの増加量で表せる
- x座標やy座標が与えられていたら、1次関数の式に代入することで傾き・切片を出せることを知らない
- 通る2点の座標が与えられている場合の解き方を知らない
- 「平行」な2直線の傾きは等しい
- ⅹ軸上にある点のy座標は0である
- y軸上にある点のx座標は0である
といったことの暗記・理解ができているかどうかを塾では確認します。
数学に苦手意識を持っている子は、こういった「問題を解くために必要最低限押さえておかなければならない知識」を文章やグラフを見ながら自分の頭の中で整理することに苦労をしています。
覚えようとしても何も頭に入ってこないから、勉強をしようとしても何をすればいいのか分からず放置
その結果さらに分からなくなって手が付けられない状態になっていくわけです。
しかし、上記で述べた基本的な事項は決して難しいものではなく、よほどのことがない限り誰でも理解できる内容です。
入塾前は数学に苦手意識を持っていた子も、塾で一緒に学び、繰り返し練習するうちに、いつの間にか頭の中が整理されていきます。
そして、「どうしてこんな簡単なことが以前はできなかったんだろう?」となっていきます。
結局、苦手意識を持った子は拒否反応から問題を解こうとすらせずに「できない」「難しい」と諦めていることが多いだけなんです。
数学を苦手にしている子が、基本的なことがある程度分かるようになった後、次につまずくのは以下のような問題です。
「下の図で、直線l・mはそれぞれy=x+4、y=-x+bの一次関数のグラフです。点Aは直線l・mの交点でその座標はA(2,6)。直線l・mとⅹ軸の交点をそれぞれB、Cとする。点Aを通り、△ABCの面積を2等分する直線の式を求めなさい。
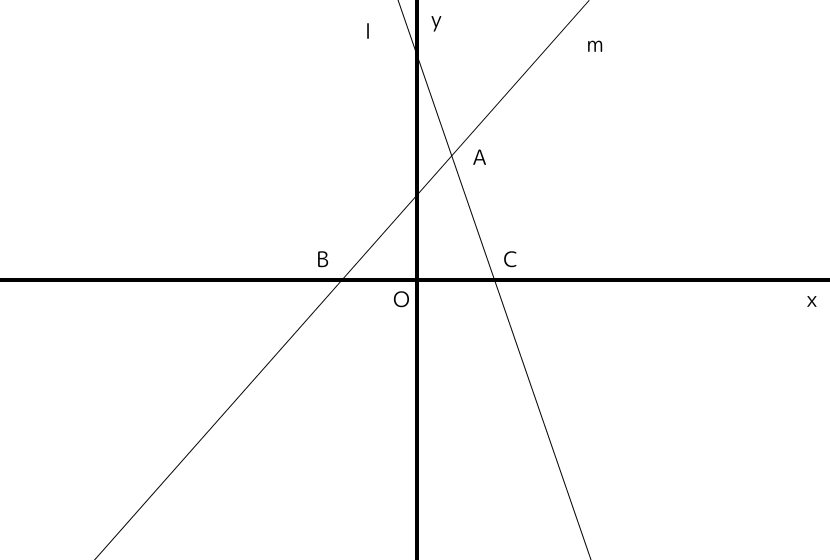
この問題は「点Aと線分BCの中点を通る直線の式を求める」ことで答えを出せるのですが
数学が得意だと
- 三角形を二等分するにはBCの中点を通ればいい
- B・Cの座標が分からなければ中点を出せないからB・Cの座標を出そう
- B・Cはⅹ軸上にあるからy=0なので、直線の式のyに0を代入してx座標を出せばいい
- 直線mは切片が分かっていないからyに0を代入してもⅹは分からないからまずは切片を出す必要がある
- 点Aの座標が与えられているからそれらをy=-x+bに代入すれば切片が分かる
1次関数の問題を解くために必要な知識を基にこのようなことを頭の中で考えられます。
授業で説明をしなくても問題が解けてしまうので「はい解いて」とすぐに問題を解いてもらい
答え合わせのときに「なんでそういう答えになったかみんなに説明してみて」と尋ね、本当に理解できているかどうかの確認をしてすぐに次の内容に進められます。
数学が苦手だと、一つ一つ手順を追っていく必要があります。
少し読みにくいですが数学が苦手な子に対して私が上の問題の解説授業をするときにやっていることを書いておきます。
「点Aを通って二等分する直線ってどこを通るかわかる?」と尋ねるとかなりの確率で「分かりません」と答えが返ってきます。
そこで「三角形を二等分するには頂点Aに向かい合う線分BCの真ん中を通ればいい」ということを図を用いて説明をします。
次に「中点を通ることが分かったけど、B・Cの中点って分かる?」と尋ねますが、ほぼ確実に「分からない」の返事が返ってくるので
「BとCの中点を求めたいけど分からないんだよね?なんでわからないの?」といった質問をし「BとCの座標が分からないとダメだ」と気づかせ
その後「じゃあ、Bの座標は何?」と尋ねると、また「分からない」と返事が返ってくるので
ⅹ軸上にあるときはどんな時でもy座標が0になるということをグラフを使って説明し
「yが0ということが分かればx座標は出せるよね?」と尋ねると「分からない」となるので
この問題を解く前に1次関数の問題を解くときにどうやっていたのかの説明をして、yに0を代入することに気づかせます。
くどくなりすぎたのでここで止めますが
このように、数学を苦手にしている子は「知識を持っていたとしてもそれをどのように使っていいのか分からない」から問題が解けないのです。
知識をどのように使えばいいかわからない状況を乗り越えるために、覚えた知識をどのように使っていくか、その思考過程を一緒に辿っていくのが塾講師として私がやっていることです。
こうすることで、少しずつ知識の使い方が分かってくるので、数学への拒否反応が徐々に減り、初見の問題を見ても「どうやったら答えを導き出せるだろうか?」と自分で考えられるようになっていくことが多いです。
もちろん問題を解く手順を一方的に教えて、教えた手順通りに問題を解かせる方が生徒にとって負担が少ないですし、「分かりやすい」「教え方上手」「できるようになった」と感じ(勘違い)させられるのは分かっています。
しかし、そんな授業をしても定期テストでは結果を出せるようになるかもしれませんが、入試で高得点を取れるようにはなりません。
定期テストで平均点を取るだけで満足できるのならそれでもいいかもしれませんが、
10代前半という「自分の能力を高めるために貴重な時期」に単なる暗記や目先の結果だけを求めて勉強をするのはもったいなさすぎるので
レイズでは、勉強に苦手意識を持っている子どもたちにも考えさせる授業を行っています。
中学の数学は難しい?

